De kern
-
De bekende ezelsbruggetjes SPIN (hoge SPecificiteit rules IN) en SNOUT (hoge SeNsitiviteit rules OUT) zijn van beperkte waarde.
-
Kennis van de prevalentie van de aandoening in de geteste populatie is essentieel om een testuitslag goed te kunnen interpreteren.
De Voorsteschuifladetest
Aios en opleider bespreken een artikel over de diagnostische waarde van de voorsteschuifladetest bij een vermoeden van een voorstekruisbandruptuur. Het artikel meldt dat de sensitiviteit van de voorsteschuifladetest 67% is, en de specificiteit 88%. De opleider vraagt de aios voor welk doel de voorsteschuifladetest het meest geschikt is. Welk antwoord is correct?
A. Voor het aantonen van een ruptuur.
B. Voor het uitsluiten van een ruptuur.
De vragenstellers hebben duidelijk de bedoeling om naar de ezelsbruggetjes SPIN en SNOUT te vragen. SPIN: bij een hoge specificiteit helpt een positieve testuitslag om de ziekte aan te tonen. SNOUT: bij een hoge sensitiviteit helpt een negatieve testuitslag om de ziekte uit te sluiten. Maar klopt dat wel?
Hoe zat het ook alweer? Sensitiviteit en specificiteit zijn de bekendste eigenschappen van een diagnostische test. Sensitiviteit staat voor het deel van de mensen dat de ziekte heeft en ook een positieve testuitslag krijgt, specificiteit staat voor het deel dat de ziekte niet heeft en ook een negatieve testuitslag krijgt [tabel].
Maar sensitiviteit en specificiteit zijn niet de enige kenmerken die ertoe doen. Degene die de test uitvoert, is op dat moment nog niet op de hoogte van de diagnose, anders was de test immers niet nodig. De vraag waar de testuitvoerder voor staat is: wat zegt de uitslag van mijn test? Stel dat de testuitslag positief is, hoe groot is dan de kans dat de patiënt ook echt de ziekte heeft? Dit noemen we de positief voorspellende waarde. Daartegenover staat de negatief voorspellende waarde: hoe groot is de kans dat de patiënt niet ziek is als de testuitslag negatief is?
Kennis van de prevalentie is cruciaal
Om de positief en de negatief voorspellende waarde te bepalen moet men in de eerste plaats de sensitiviteit en specificiteit van de test kennen, bij voorkeur voor de setting waarin de test wordt uitgevoerd. Maar ook moet men de verhouding kennen tussen het aantal zieken en het aantal niet-zieken binnen de geteste populatie. In deze context spreken we vaak van de ‘prevalentie’ van de aandoening. Om verwarring te voorkomen: het gaat hier niet om de prevalentie in de bevolking, maar om de prevalentie bij de mensen bij wie de test wordt afgenomen.
Ik werk twee voorbeelden uit van een test die, net als in de kennistoetsvraag, een sensitiviteit heeft van 67% en een specificiteit van 88% en die uitgevoerd wordt in twee verschillende populaties, met prevalenties van respectievelijk 50% en 10%.
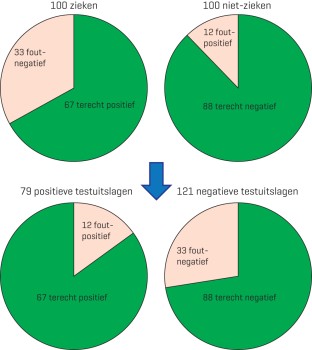
Bij een prevalentie van 50%, dus wanneer de helft van de geteste populatie ziek is, is de positief voorspellende waarde 67/79, dat wil zeggen 85% van de positief getesten is daadwerkelijk ziek [figuur 1]. De negatief voorspellende waarde is 88/121, dat wil zeggen 73% van de negatief getesten is daadwerkelijk niet ziek. Bij deze prevalentie helpt een hoge specificiteit dus inderdaad om de ziekte aan te tonen: de positief voorspellende waarde is groter dan de negatief voorspellende waarde. Antwoord ‘A’ zou correct zijn.
Figuur 1 | Sensitiviteit 67% en specificiteit 88% bij een prevalentie van 50%
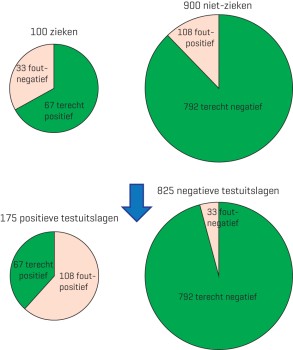
Hoe anders wordt het beeld als de prevalentie niet 50% is, maar slechts 10%. De positief voorspellende waarde is nu 67/175, dus slechts 38% van de positief getesten is daadwerkelijk ziek. De negatief voorspellende waarde is 792/825, dus van de mensen met een negatieve testuitslag is maar liefst 96% daadwerkelijk niet ziek [figuur 2]. Bij deze lage prevalentie is de specificiteit onvoldoende: doordat een veel groter deel van de geteste mensen niet ziek is, gooien de maar liefst 108 foutpositieven roet in het eten. Het gevolg is dat het merendeel van de mensen met een positieve testuitslag geen ziekte heeft. We hebben nu meer aan de negatieve testuitslagen, antwoord ‘A’ van de kennistoetsvraag is dus onjuist.
Figuur 2 | Sensitiviteit 67% en specificiteit 88% bij een prevalentie van 10%
Wees voorzichtig!
De oorspronkelijke publicatie waarin SPIN en SNOUT werden geïntroduceerd (volledigheidshalve: als SpPin en SnNout) vermeldt wel dat beide ezelsbruggetjes alleen bruikbaar zijn bij tests met een zeer hoge specificiteit of sensitiviteit. 1 Maar ook dan kan men zich situaties voorstellen waarin een extreem lage of hoge prevalentie de gebruiker op het verkeerde been zet. Wanneer het ezelsbruggetje nog wel opgaat en wanneer niet meer, hangt af van de balans tussen sensitiviteit en specificiteit enerzijds en de prevalentie anderzijds. Vuistregels hiervoor zijn mij niet bekend. Wanneer de prevalentie bij benadering bekend is, is het niet zo moeilijk om zelf de 2 × 2-tabel te maken en de voorspellende waarden te berekenen.
Concluderend: de vraag uit de kennistoets gaf onvoldoende informatie. Welk antwoord juist is, hangt mede af van de verhouding tussen het aantal zieken en niet-zieken in de geteste populatie. Bovendien waren de gekozen sensitiviteit en specificiteit niet erg hoog. Laten we SPIN en SNOUT voortaan beschouwen als krakkemikkige ezelsbruggetjes, te betreden op eigen risico.
| Ziekte aanwezig | Ziekte afwezig | Totaal | |
|---|---|---|---|
| Test positief | ATerecht positief | BFout-positief | Alle mensen met een positieve testuitslag |
| Test negatief | CFout-negatief | DTerecht negatief | Alle mensen met een negatieve testuitslag |
| Totaal | Alle mensen met de ziekte | Alle mensen zonder de ziekte | Alle mensen die getest zijn |
Literatuur
- 1.↲Sackett DL, Straus S. On some clinically useful measures of the accuracy of diagnostic tests. ACP J Club 1998;129:A17-9.